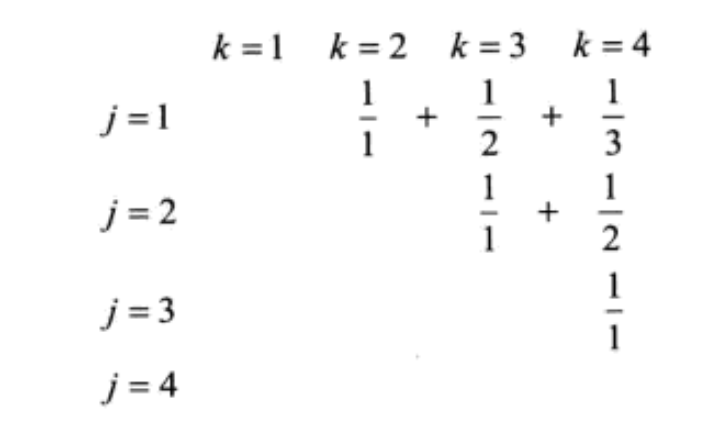第 2 章：和式

记号

求和的符号有两种形式

第一种是确定界限的形式，也叫封闭形式，例如： $\sum_{k = 1}^{n} a_{k}$

第二种叫做一般形式，就是把一个或者多个条件写在 $\sum$ 符号的下面，例如刚刚的例子可以写成 $\sum_{1 \leq k \leq n} a_{k}$

和式和递归式的转化

和式和递归式之间可以相互转化，

和式转化成递归式

$S_{n} = \sum a_{n}$ 可以转化为 $S_{n} = S_{n - 1} + a_{n}, S_{1} = a_{1}$ ，后面这一项就是一个递归式子

例如：我们这里有一个递归式

\begin{array}{r} R_{0} = α \\ R_{n} = R_{n - 1} + β + γ n, n > 0 \end{array}

这个可以写成通解的形式： $R_{n} = A (n) α + B (n) β + C (n) γ$

由成套方法得出 $A (n) = 1, B (n) = n, C (n) = (n^{2} + n) / 2$

我们需要计算 $\sum_{k = 0}^{n} (a + b k)$ ，只需要把 $a = α, a = β, b = γ$ 代入即可

递归式转化成和式

\begin{aligned} T_{0} & = 0 \\ T_{n} & = 2 T_{n - 1} + 1, n > 0 \end{aligned}

两边除以 $2^{n}$ 得到

\begin{aligned} T_{0} / 2^{0} & = 0 \\ T_{n} / 2^{n} & = T_{n - 1} / 2^{n - 1} + 1 / 2^{n}, n > 0 \end{aligned}

设 $S_{n} = T_{n} / 2^{n}$

\begin{aligned} S_{0} & = 0 \\ S_{n} & = S_{n - 1} + 1 / 2^{n}, n > 0 \end{aligned}

由此得到 $S_{n} = \sum_{k = 1}^{n} {\frac{1}{2}}^{k} = 1 - (\frac{1}{2})^{n}$ ，所以 $T_{n} = 2^{n} - 1$

和式的变换法则

经典的三条性质，注意这里的 $K$ 是一个集合

\sum_{k \in K} c a_{k} = c \sum_{k \in K} a_{k} (分配律)

\sum_{k \in K} (a_{k} + b_{k}) = \sum_{k \in K} a_{k} + \sum_{k \in K} b_{k} (结合律)

\sum_{k \in K} a_{k} = \sum_{p (k) \in K} a_{p (k)} (交换律)

注意 $p (k)$ 是一个双射函数，也可以理解为一个排列

例如： $K = {1, 2, 3, 4}$ 那么， $p (k) = {4, 2, 3, 1}$ 就是一个排列

当然 $p (k)$ 可以多出几个元素例如上面那个例子 $p (k) = {4, 2, 3, 1, 5, 6}$ 也是可以的， $5, 6$ 不在 $K$ 中

接下来看一个例子： $S = \sum_{0 \leq k \leq n} (a + b k)$

利用交换率，用 $n - k$ 代替 $k$ ，得到

S = \sum_{0 \leq n - k \leq n} (a + b (n - k)) = \sum_{0 \leq k \leq n} (a + b n - b k)

利用结合律，把这两个方程相加，得到

2 S = \sum_{0 \leq k \leq n} (a + b k + a + b n - b k) = \sum_{0 \leq k \leq n} (2 a + b n) = (n + 1) (2 a + b n)

所以

S = \frac{(n + 1) (2 a + b n)}{2}

扰动法

和式中有一种非常厉害的方法叫扰动法，就是把一项从和式中去除出去，然后尝试把剩下的项变成 $S_{n}$ 的形式，从而解出 $S_{n}$

例如： $S_{n} = \sum_{0 \leq k \leq n} a x^{k}$ ，使用扰动法的基本套路

S_{n} + a x^{n + 1} = a x^{0} + \sum_{1 \leq k \leq n + 1} a x^{k} = a x^{0} + \sum_{0 \leq k \leq n} a x^{k + 1} = a x^{0} + x S_{n}

等式两边同时出现了 $S_{n}$ ，解出 $S_{n} = \frac{a - a x^{n + 1}}{1 - x}$

考虑另外一个例子： $S_{n} = \sum_{0 \leq k \leq n} k 2^{k}$ ，考虑扰动法

\begin{aligned} S_{n} + (n + 1) 2^{n + 1} & = \sum_{0 \leq k \leq n} (k + 1) 2^{k + 1} \\ = 2 \sum_{0 \leq k \leq n} k 2^{k} + \sum_{0 \leq k \leq n} 2^{k + 1} \\ = 2 S_{n} + 2^{n + 2} - 2 \end{aligned}

解出 $S_{n} = 2^{n + 1} (n - 1) + 2$

设未知数 $x$ ，能求出 $S_{n} = \sum_{0 \leq k \leq n} k x^{k}$ 的通解：

S_{n} = \frac{x - x^{n + 1} (n + 1) + n x^{n + 2}}{(x - 1)^{2}}, x \neq 1

我们也可以利用求导的方法，求出 $S_{n} = \sum_{0 \leq k \leq n} k x^{k}$ 的通解：

已知： $\sum_{k = 0}^{n} x^{k} = \frac{1 - x^{n + 1}}{1 - x}$ ，两边同时求导

\sum_{k = 0}^{n} k x^{k - 1} = \frac{(1 - x) (- (n + 1) x^{n}) + 1 - x^{n + 1}}{(1 - x)^{2}} = \frac{1 - (n + 1) x^{n} + n x^{n + 1}}{(1 - x)^{2}}

两边同时乘以 $x$ ，得到

\sum_{k = 0}^{n} k x^{k} = \frac{x - x^{n + 1} (n + 1) + n x^{n + 2}}{(x - 1)^{2}}

就能得到和上面扰动法一样的结果了

多重和式

多重和式对应于连续函数的积分，可以利用积分的一些思维来思考多重和式

对于自变量相互无关的情况很好理解

\begin{aligned} \sum_{1 \leq j, k \leq 3} a_{j} b_{k} & = a_{1} b_{1} + a_{1} b_{2} + a_{1} b_{3} + a_{2} b_{1} + a_{2} b_{2} + a_{2} b_{3} + a_{3} b_{1} + a_{3} b_{2} + a_{3} b_{3} \\ = a_{1} (b_{1} + b_{2} + b_{3}) + a_{2} (b_{1} + b_{2} + b_{3}) + a_{3} (b_{1} + b_{2} + b_{3}) \\ = (a_{1} + a_{2} + a_{3}) (b_{1} + b_{2} + b_{3}) \\ = (\sum_{1 \leq j \leq 3} a_{j}) (\sum_{1 \leq k \leq 3} b_{k}) \end{aligned}

一个多重和式可以转化成两个和式相乘的形式，前提是 $J = K$ ，其中 $j \in J, k \in K$ ，这一点在级数相乘的时候极为有效

在具体求多重和式的时候，往往是一层一层往外求，理论上来说，先固定住哪个自变量都是无所谓的，所以我们可以交换求和符号的位置

设 $P (j, k)$ 返回的是 $j, k$ 是否满足某种性质，那么有：

\sum_{j \in J} \sum_{k \in K} a_{j, k} [P (j, k)] = \sum_{k \in K} \sum_{j \in J} a_{j, k} [P (j, k)]

讨论自变量之间有某些限制

一种比较常见的方式： $1 \leq j \leq k \leq n$ ，我们可以通过画图找出需要求和的元素

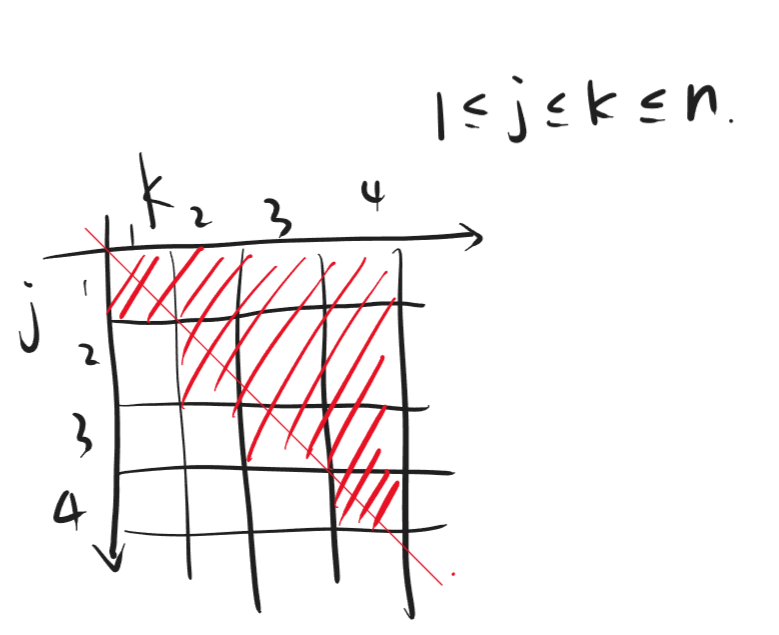
可以看到对角线以及右上角的那一块都是需要求和的

另外一种常见的方式 $1 \leq j, k \leq n, j + k = n$ ，画出图来是按对角线求和

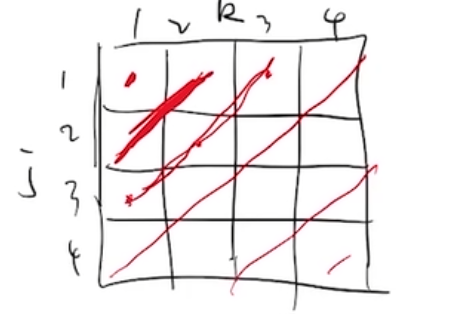
这种求和方法有一种自己的名字，叫卷积（Convolution）

例一：求 $\sum_{1 \leq j \leq k \leq n} a_{j} a_{k}$

可以看到要求部分是右上三角形

由于图标的对称性，可以得到 $S_{左下} = S_{右上}$

由容斥原理： $S_{左下} + S_{右上} = S_{全部} - S_{对角线}$

于是就能得我们想要的答案了

S_{右上} = \sum_{1 \leq j \leq k \leq n} a_{j} a_{k} = \frac{1}{2} ({(\sum_{k = 1}^{n} a_{k})}^{2} + \sum_{k = 1}^{n} a_{k}^{2})

例二：求 $S = \sum_{1 \leq j < k \leq n} (a_{k} - a_{j}) (b_{k} - b_{j})$

交换 $j, k$ 仍然由对称性：

S = \sum_{1 \leq k < j \leq n} (a_{j} - a_{k}) (b_{j} - b_{k}) = \sum_{1 \leq k < j \leq n} (a_{k} - a_{j}) (b_{k} - b_{j})

所以得到答案

2 S = \sum_{1 \leq j, k \leq n} (a_{j} - a_{k}) (b_{j} - b_{k}) - \sum_{1 \leq j = k \leq n} (a_{j} - a_{k}) (b_{j} - b_{k})

显然，第二个和式等于 $0$ ，把第一个和式展开

\begin{aligned} 2 S & = \sum_{1 \leq j, k \leq n} a_{j} b_{j} - \sum_{1 \leq j, k \leq n} a_{j} b_{k} - \sum_{1 \leq j, k \leq n} a_{k} b_{j} + \sum_{1 \leq j, k \leq n} a_{k} b_{k} \\ = 2 n \sum_{1 \leq k \leq n} a_{k} b_{k} - 2 (\sum_{k = 1}^{n} a_{k}) (\sum_{k = 1}^{n} b_{k}) \end{aligned}

所以就得出了 $S = n \sum_{1 \leq k \leq n} a_{k} b_{k} - (\sum_{k = 1}^{n} a_{k}) (\sum_{k = 1}^{n} b_{k})$

若 ${a}, {b}$ 都是升序的，那么显然 $S \geq 0$ ，所以 $n \sum_{1 \leq k \leq n} a_{k} b_{k} - (\sum_{k = 1}^{n} a_{k}) (\sum_{k = 1}^{n} b_{k}) \geq n$
，可以推出不等式： $n \sum_{1 \leq k \leq n} a_{k} b_{k} \geq (\sum_{k = 1}^{n} a_{k}) (\sum_{k = 1}^{n} b_{k})$
若 ${a}$ 是升序的， ${b}$ 是降序的，那么显然 $S \leq 0$ ，所以 $n \sum_{1 \leq k \leq n} a_{k} b_{k} - (\sum_{k = 1}^{n} a_{k}) (\sum_{k = 1}^{n} b_{k}) \leq n$
，可以推出不等式： $n \sum_{1 \leq k \leq n} a_{k} b_{k} \leq (\sum_{k = 1}^{n} a_{k}) (\sum_{k = 1}^{n} b_{k})$

这两个不等式叫做 切比雪夫单调不等式

例三

S_{n} = \sum_{1 \leq j < k \leq n} \frac{1}{k - j}

我们可以用 $k - j$ 替换 $j$ ，然后固定 $k$

\begin{aligned} S_{n} & = \sum_{1 \leq k \leq n} \sum_{1 \leq j \leq k} \frac{1}{k - j} \\ = \sum_{1 \leq k \leq n} \sum_{0 \leq j \leq k - 1} \frac{1}{j} \\ = \sum_{1 \leq k \leq n} H_{k - 1} \\ = \sum_{0 \leq k \leq n - 1} H_{k} \end{aligned}

其中 $H_{k}$ 是调和级数，我们对调和级数有公式，但是对于调和级数求和没有公式，说明固定 $k$ 走不通考虑固定 $j$

\begin{aligned} S_{n} & = \sum_{1 \leq j < n} \sum_{j < k \leq n} \frac{1}{k - j} \\ = \sum_{1 \leq j \leq n} \sum_{j < k + j \leq n} \frac{1}{k + j - j} \\ = \sum_{1 \leq j \leq n} \sum_{0 < k \leq n - j} \frac{1}{k} \\ = \sum_{1 \leq j \leq n} H_{n - j} \\ = \sum_{0 \leq j \leq n - 1} H_{j} \end{aligned}

还是回到了调和级数求和的问题，考虑按对角线求和

\begin{aligned} S_{n} & = \sum_{1 \leq j < n} \sum_{j < k \leq n} \frac{1}{k - j} \\ = \sum_{1 \leq j \leq n} \sum_{j < k + j \leq n} \frac{1}{k + j - j} \\ = \sum_{1 \leq j \leq n} \sum_{0 < k \leq n - j} \frac{1}{k} \\ = \sum_{0 < k < n} \sum_{1 \leq j \leq n - k} \frac{1}{k} \\ = \sum_{0 < k < n} \frac{n - k}{k} = \sum_{0 < k < n} (\frac{n}{k} - 1) \\ = n \sum_{1 \leq k \leq n} \frac{1}{k} - \frac{n}{n} - (n - 1) \\ = n H_{n} - n \end{aligned}

我们还可以从几何的层面来理解这个式子：

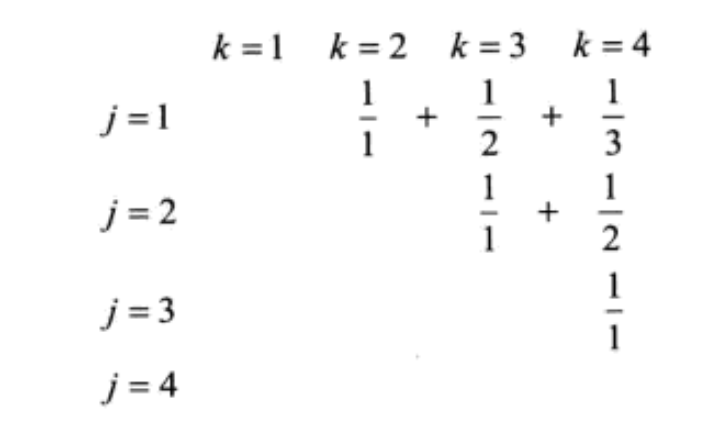
刚开始的几次我们按照行和列求和，都会得到一个调和级数求和的式子，最后一种方式是按照对角线，这里得到 $\frac{3}{1} + \frac{2}{2} + \frac{1}{3}$

一般性方法

这一节基本上就是总结性质的，把前面介绍的方法综合运用一下

要求一个立方和 $S_{n} = \sum_{k = 0}^{n} k^{2}, n \geq 0$

方法0：查找公式

OEIS 能帮我们很好的查找公式

得到的答案是 $S_{n} = \frac{n (n + 1) (2 n + 1)}{6}$

方法1：数学归纳法

已知： $S_{n} = \frac{n (n + \frac{1}{2}) (n + 1)}{3}$

显然 $S_{0} = 0$ 成立，假设 $n > 0$ 时， $S_{n - 1} = \frac{(n - 1) (n - \frac{1}{2}) n}{3}$ 成立，有： $S_{n} = S_{n - 1} + S$

\begin{aligned} 3 S_{n} & = (n - 1) (n - \frac{1}{2}) (n) + 3 n^{2} \\ = n^{3} + \frac{3}{2} n^{2} + \frac{1}{2} n \\ = n (n + 1) (n + \frac{1}{2}) \end{aligned}

所以 $S_{n} = \frac{n (n + \frac{1}{2}) (n + 1)}{3}$ 对所有 $n \geq 0$ 都成立

方法2：扰动法

\begin{aligned} S_{n} + (n + 1)^{2} & = \sum_{k = 0}^{n} (k + 1)^{2} = \sum_{k = 0}^{n} (k^{2} + 2 k + 1) \\ = \sum_{k = 0}^{n} k^{2} + 2 \sum_{k = 0}^{n} k + \sum_{k = 0}^{n} 1 \\ = S_{n} + 2 \sum_{k = 0}^{n} k + n + 1 \end{aligned}

惊人的发现，我们需要求的 $S_{n}$ 被消掉了，留下一个 $\sum_{k = 0}^{n} k = \frac{(n + 1)^{2} - (n + 1)}{2} = \frac{n (n + 1)}{2}$

我们猜想能不能用立方和来把平方和求出来，设 $T_{n} = \sum_{k = 0}^{n} k^{3}$

\begin{aligned} T_{n} + (n + 1)^{3} & = \sum_{k = 0}^{n} (k + 1)^{3} = \sum_{k = 0}^{n} (k^{3} + 3 k^{2} + 3 k + 1) \\ = \sum_{k = 0}^{n} k^{3} + 3 \sum_{k = 0}^{n} k^{2} + 3 \sum_{k = 0}^{n} k + \sum_{k = 0}^{n} 1 \\ = T_{n} + 3 S_{n} + 3 \frac{n (n + 1)}{2} + n + 1 \end{aligned}

$T_{n}$ 被消掉了，留下我们需要求的 $S_{n}$ ，这样 $3 S_{n} = (n + 1)^{3} - 3 \frac{n (n + 1)}{2} - (n + 1)$

所以 $S_{n} = \frac{n (n + 1) (n + \frac{1}{2})}{3}$

方法3：建立成套方法

还是老规矩，建立成套方法，设：

\begin{aligned} R_{0} & = α, n = 0 \\ R_{n} & = R_{n - 1} + β + γ n + δ n^{2}, n > 0 \end{aligned}

解的一般形式就是： $R_{n} = A (n) α + B (n) β + C (n) γ + D (n) δ$

我们已知， $δ = 0$ 时， $A (n) = 1, B (n) = n, C (n) = (n^{2} + n) / 2$

现在要求 $D (n)$ 和他们的关系，设 $R_{n} = n^{3}$ ，有 $n^{3} = (n - 1)^{3} + β + γ n + δ n^{2}$

可得： $α = 0$ ， $β = 1$ ， $γ = - 3$ ， $δ = 3$ ，代入： $3 D (n) - 3 C (n) + B (n) = n^{3}$

就把 $D (n)$ 接出来了， $D (n) = n^{3} - 3 \frac{n (n + 1)}{2} + n = \frac{n (n + \frac{1}{2}) (n + 1)}{3}$

我们需要求的和式 $S_{n}$ 转化成递归式子，只需要令 $α = β = γ = 0$ 以及 $δ = 1$

则 $S_{n} = D (n)$

方法4：用积分替换和式

我们已知 $\int_{0}^{n} x^{2} d x = \frac{n^{3}}{3}$ ，显然，和式和积分之间的差距并不差，只是差一个误差

我们设这个误差为 $E_{n} = S_{n} - \frac{n^{3}}{3}$ ，通过 $S_{n}$ 的递归式，我们能得出 $S_{n} = S_{n - 1} + n^{2}$

\begin{aligned} E_{n} & = S_{n} - \frac{n^{3}}{3} = S_{n - 1} + n^{2} - \frac{n^{3}}{3} \\ = E_{n - 1} + \frac{(n - 1)^{3}}{3} + n^{2} - \frac{n^{3}}{3} \\ = E_{n - 1} + n - \frac{1}{3} \end{aligned}

于是，我们就得到了 $E_{n}$ 的递推式， $E_{n} = E_{n - 1} + n - \frac{1}{3}$ ， $E_{0} = 0$

很容易算出 $E_{n}$ 的通项公式为 $E_{n} = \frac{n (n + 1)}{2} - \frac{n}{3}$ ，所以 $S_{n} = E_{n} + \frac{n^{3}}{3} = \frac{n (n + 1) (n + \frac{1}{2})}{3}$

方法5：展开和放缩

这种方法极具技巧性，把一个一重和式转化成二重和式

\begin{aligned} S_{n} & = \sum_{k = 0}^{n} k^{2} = \sum_{1 \leq j \leq k \leq n} k \\ = \sum_{1 \leq j \leq n} \sum_{j \leq k \leq n} k \\ = \sum_{1 \leq j \leq n} (\frac{j + n}{2}) (n - j + 1) \\ = \frac{1}{2} \sum_{1 \leq j \leq n} (n (n + 1) + j - j^{2}) \\ = \frac{1}{2} n^{2} (n + 1) + \frac{1}{4} n (n + 1) - \frac{1}{2} S_{n} \end{aligned}

这样等式两边都出现了 $S_{n}$ ，解出 $S_{n} = \frac{n (n + 1) (2 n + 1)}{6}$

有限微积分

我们类似于积分和微分的思维，在离散域上定义有限微积分，定义差分算子 $Δ f (x)$ 是 $(f (x + h) - f (x)) / h$ 当 $h = 1$ 时的值

还需要定义两种特殊的次幂:

下降阶乘幂 $x^{\underset{―}{m}} = x (x - 1) \dots (x - m + 1), m \geq 0$
上升阶乘幂 $x_{\overset{―}{m}} = x (x + 1) \dots (x + m - 1), m \geq 0$

我们为什么要定义这样奇特的形式呢，因为这样求差分的时候会和微分有很多共同点

\begin{aligned} Δ x^{\underset{―}{m}} & = (x + 1)^{\underset{―}{m}} - x^{\underset{―}{m}} \\ = (x + 1) x (x - 1) \dots (x - m + 2) - x (x - 1) (x - 2) \dots (x - m + 1) \\ = (x + 1 - (x - m + 1)) x (x - 1) (x - 2) \dots (x - m + 2) \\ = m x (x - 1) (x - 2) \dots (x - m + 2) \\ = m x^{\underset{―}{m - 1}} \end{aligned}

有限微积分也存在类似于微积分基本定理的东西

g (x) = Δ f (x) ⟺ \sum g (x) δ x = f (x) + C

这里的 $\sum g (x) δ x$ 是 $g (x)$ 的不定和式，这里的 $C$ 可以是周期为 $1$ 的任意函数

大名鼎鼎的牛顿-莱布尼茨公式在有限微积分中也有体现 $\sum_{a}^{b} g (x) δ x = f (x) |_{a}^{b} = f (b) - f (a)$

思考 $\sum_{a}^{b} g (x) δ x = f (x) |_{a}^{b} = f (b) - f (a)$ 当，上下限相同时：

\sum_{a}^{a} g (x) δ x = f (x) |_{a}^{a} = f (a) - f (a) = 0

当上下限差 $1$ 时：

\sum_{a}^{a + 1} g (x) δ x = f (x) |_{a}^{a + 1} = f (a + 1) - f (a) = Δ f (x) = g (x)

着预示着和传统的求和符号有点不同，可以理解为 $\sum_{a}^{b} g (x) δ x = \sum_{k = a}^{b - 1} g (k) = \sum_{a \leq k < b} g (k), b \geq a$

也就是说，如果存在能找到一个 $f (x)$ 使得 $f (x + 1) - f (x) = g (x)$ ，那么理论上来说就可以求 $\sum g (x)$ 这类的和了

我们尝试去求类似于原函数的东西 $f (x)$

比如： $g (x) = x^{\underset{―}{m}}$ ， $f (x) = \frac{x^{\underset{―}{m + 1}}}{m + 1}$

我们用前面的例子，求 $\sum_{0 \leq k < n} k^{2}$ 已知 $k^{2} = k^{\underset{―}{2}} + k^{\underset{―}{1}}$ ，所以

\sum_{0 \leq k < n} k^{2} = \frac{n^{\underset{―}{3}}}{3} + \frac{n^{\underset{―}{2}}}{2} = n (n - 1) (n - 2 + \frac{3}{2}) = \frac{1}{3} n (n - \frac{1}{2}) (n - 1)

利用 $n + 1$ 替换 $n$ 就可以得到 $S_{n}$ 了

尝试继续推广无限微积分，考虑下降次幂为负数的情况， $x^{\underset{―}{m}}, m < 0$

观察:

$x^{\underset{―}{3}} = x (x - 1) (x - 2)$ ， $x^{\underset{―}{2}} = x (x - 1)$ 两个相除得出 $x - 2$
$x^{\underset{―}{2}} = x (x - 1)$ ， $x^{\underset{―}{1}} = x$ 两个相除得出 $x - 1$
$x^{\underset{―}{1}} = x$ ， $x^{\underset{―}{0}} = 1$ 两个相除得出 $x$

于是找规律得出 $x^{\underset{―}{- 1}} = \frac{1}{x + 1}, x^{\underset{―}{- 2}} = \frac{1}{(x + 1) (x + 2)}$ ， $x^{- m} = \frac{1}{(x + 1) (x + 2) \dots (x + m)}$

通常的幂法则： $x^{m + n} = x^{m} x^{n}$ ，推广到有限微积分就变成了 $x^{\underset{―}{m + n}} = x^{\underset{―}{m}} (x - m)^{\underset{―}{n}}$

现在确认下降幂的差分性质在 $m < 0$ 是否成立也就是 $Δ x^{\underset{―}{m}} = m x^{\underset{―}{m - 1}}$

如果 $m = - 2$ ，有

\begin{aligned} Δ x^{\underset{―}{- 2}} & = (x + 1)^{\underset{―}{- 2}} - x^{\underset{―}{- 2}} \\ = \frac{1}{(x + 2) (x + 3)} - \frac{1}{(x + 1) (x + 2)} \\ = \frac{(x + 1) - (x + 3)}{(x + 1) (x + 2) (x + 3)} \\ = \frac{- 2}{(x + 1) (x + 2) (x + 3)} \\ = - 2 x^{\underset{―}{- 3}} \end{aligned}

说明求和性质对 $m < 0$ 也成立，即 $\sum_{a}^{b} x^{\underset{―}{m}} δ x = \frac{x^{\underset{―}{m + 1}}}{m + 1} |_{a}^{b}, m \neq 1$

现在考虑 $m = 1$ 的时候，对于微积分，我们又 $\int_{a}^{b} x^{- 1} d x = \ln x |_{a}^{b}$

我们需要在有限微积分中找一个类似于 $\ln x$ 的函数，这个函数的差分为 $\frac{1}{x + 1}$

很显然能得到这个函数就是 $H_{x}$ ，于是就得到了求和的完整形式

\sum_{a}^{b} x^{- m} δ x = {\begin{cases} {\frac{x^{m + 1}}{m + 1} |}_{a}^{b}, & m \neq - 1, \\ {H_{x} |}_{a}^{b}, & m = - 1. \end{cases}

类似的，我们需要找一个 $e^{x}$ 类似物，根据定义 $d (e^{x}) = e^{x}$ ，所以有 $f (x + 1) - f (x) = f (x) ⟺ f (x + 1) = 2 f (x)$ ，即 $f (x) = 2^{x}$

$c^{x}$ 的差分也相当简单，即对任意的 $c$ 有

Δ (c^{x}) = c^{x + 1} - c^{x} = (c - 1) c^{x} .

那么， $c \neq 1$ 时， $c^{x}$ 的原函数就是 $c^{x} / (c - 1)$

两个相乘的函数求微分： $d (u v) = u d v + v d u$ ，两边同时积分得到分部积分法的公式： $\int u d v = u v - \int v d u$

有限微积分也类似

\begin{aligned} Δ (u (x) v (x)) & = u (x + 1) v (x + 1) - u (x) v (x) \\ = u (x + 1) v (x + 1) - u (x) v (x + 1) + u (x) v (x + 1) - u (x) v (x) \\ = u (x) Δ v (x) + v (x + 1) Δ u (x) . \end{aligned}

这里的 $v (x + 1)$ 看着很烦，所以定义一个位移算子 $E f (x) = f (x + 1)$

所以乘积差分法则可以写为：

Δ (u v) = u Δ v + E v Δ u

两边求和得：

\sum u Δ v = u v - \sum E v Δ u

有限微积分和无限微积分对应着离散和连续，有很多共通点，在下列表中给出

image.png|789

来看几个例子：

例一：

\begin{aligned} \sum_{k = 0}^{n} k 2^{k} & = \sum_{0}^{n + 1} x 2^{x} δ x \\ = x 2^{x} - 2^{x + 1} |_{0}^{n + 1} \\ = ((n + 1) 2^{n + 1} - 2^{n + 2}) - (0 \times 2^{0} - 2^{1}) \\ = (n - 1) 2^{n + 1} + 2 \end{aligned}

例二： 求 $\sum_{0 \leq k < n} k H_{k}$

先求原函数，根据分部积分法则：

\begin{aligned} \sum x H_{x} δ x & = \frac{x^{\underset{―}{2}}}{2} H_{x} - \sum \frac{(x + 1)^{\underset{―}{2}}}{x} x^{\underset{―}{- 1}} δ x \\ = \frac{x^{\underset{―}{2}}}{2} H_{x} - \frac{1}{2} \sum x^{\underset{―}{1}} δ x \\ = \frac{x^{\underset{―}{2}}}{2} H_{x} - \frac{x^{\underset{―}{2}}}{4} + C \end{aligned}

然后把上下限代入：

\sum_{0 \leq k < n} k H_{k} = \sum_{0}^{n} x H_{x} δ x = \frac{n^{\underset{―}{2}}}{2} (H_{n} - \frac{1}{2})

无限和式

引用大乌拉的一句话：

我们对无穷的东西几乎一无所知

这一章书上举了几个具体的例子，都在表达无穷和式似乎没有我们想象的这么简单